
Except in the case of special triangles (such as an equilateral triangle, and one median in an isosceles triangle), you can’t construct a median with just one fold. When you construct medians, you need to do two things: First find the midpoint then fold or draw a segment connecting that point to the opposite vertex. The intersection of the crease and the original line segment is the midpoint of the line segment. Next, fold the paper so that the endpoints of the line segment overlap. To construct the midpoint of a line segment, start by drawing a line segment on the patty paper. Here is a sample construction with patty paper to get you started: Throughout this part of the session, use just a pen or pencil, your straightedge, and patty paper to complete the constructions described in the problems. Though your “straightedge” might actually be a ruler, don’t measure! Use it only to draw straight segments. Since you can see through the paper, you can use the folds to create geometric objects.

You can fold the patty paper to create creases. In the problems below, your tools will be a straightedge and patty paper. The most common tools for constructions in geometry are a straightedge (a ruler without any markings on it) and a compass (used for drawing circles). A construction is a method, while a picture merely illustrates the method. It shows how a figure can be accurately drawn with a specified set of tools. The essential element of a construction is that it is a kind of guaranteed recipe. Drawings are intended to aid memory, thinking, or communication, and they needn’t be much more than rough sketches to serve this purpose quite well. Yes, the altitude of a triangle is also referred to as the height of the triangle.Geometers distinguish between a drawing and a construction. Is the Altitude of a Triangle Same as the Height of a Triangle? Since it is perpendicular to the base of the triangle, it always makes a 90° with the base of the triangle. Yes, the altitude of a triangle is a perpendicular line segment drawn from a vertex of a triangle to the base or the side opposite to the vertex. Does the Altitude of a Triangle Always Make 90° With the Base of the Triangle? It bisects the base of the triangle and always lies inside the triangle. The median of a triangle is the line segment drawn from the vertex to the opposite side that divides a triangle into two equal parts.


It can be located either outside or inside the triangle depending on the type of triangle. The altitude of a triangle is the perpendicular distance from the base to the opposite vertex. The altitude of a triangle and median are two different line segments drawn in a triangle. What is the Difference Between Median and Altitude of Triangle? \(h= \frac\), where 'h' is the altitude of the scalene triangle 's' is the semi-perimeter, which is half of the value of the perimeter, and 'a', 'b' and 'c' are three sides of the scalene triangle. The following section explains these formulas in detail. The important formulas for the altitude of a triangle are summed up in the following table.
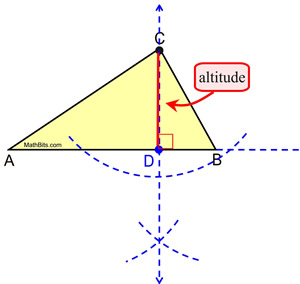
CONSTRUCTION OF AN ALTITUDE GEOMETRY HOW TO
Let us learn how to find out the altitude of a scalene triangle, equilateral triangle, right triangle, and isosceles triangle. Using this formula, we can derive the formula to calculate the height (altitude) of a triangle: Altitude = (2 × Area)/base. The basic formula to find the area of a triangle is: Area = 1/2 × base × height, where the height represents the altitude.


 0 kommentar(er)
0 kommentar(er)
